На рисунке представлен участок электрической цепи DE: где и – сопротивления. Вероятности того ч...: ответ на тест 1074216 - Теория вероятностей и математическая статистика
На рисунке представлен участок электрической цепи DE:

где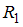 ,
, 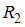 и
и 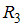 – сопротивления.
– сопротивления.
Вероятности того, что сопротивления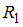 ,
, 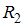 и
и  выйдут из строя в течение ближайшего часа, равны соответственно 0,4, 0,3 и 0,1. Тогда значение
выйдут из строя в течение ближайшего часа, равны соответственно 0,4, 0,3 и 0,1. Тогда значение  равно …
равно …

где
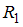 ,
, 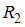 и
и 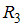 – сопротивления.
– сопротивления.Вероятности того, что сопротивления
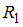 ,
, 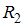 и
и  выйдут из строя в течение ближайшего часа, равны соответственно 0,4, 0,3 и 0,1. Тогда значение
выйдут из строя в течение ближайшего часа, равны соответственно 0,4, 0,3 и 0,1. Тогда значение  равно …
равно …
Вопрос задал(а): Анонимный пользователь, 13 Ноябрь 2020 в 18:18
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 18:18
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 18:18
