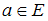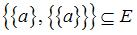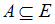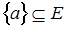Вопрос № 860247 - Математика
Дано множество
.
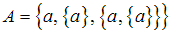Пусть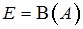
– булеан множества 
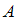, т.е. множество всех подмножеств множества 
.
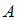Тогда истинным будет соотношение …
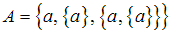.Пусть
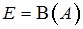– булеан множества 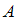, т.е. множество всех подмножеств множества 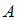.Тогда истинным будет соотношение …
Вопрос задал(а): Анонимный пользователь, 13 Ноябрь 2020 в 15:21
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 15:21
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 15:21
Похожие вопросы
Дано множество
.
Пусть
– булеан множества 
, т.е. множество всех подмножеств множества 
.
Тогда истинным будет соотношение …
.Пусть
– булеан множества , т.е. множество всех подмножеств множества .Тогда истинным будет соотношение …
Для множества 
построено множество 
, т.е. булеан множества 
(множество всех подмножеств множества 
). Из этого булеана удалили пустое множество 
и все одноэлементные множества. Полученное в результате множество обозначили символом 
и построили его булеан 
.
Тогда число элементов множества
равно …
построено множество , т.е. булеан множества (множество всех подмножеств множества ). Из этого булеана удалили пустое множество и все одноэлементные множества. Полученное в результате множество обозначили символом и построили его булеан .Тогда число элементов множества
равно … 
Другие вопросы по предмету Математика
Для множества 
построено множество 
, т.е. булеан множества 
(множество всех подмножеств множества 
). Из этого булеана удалили пустое множество 
и все одноэлементные множества. Полученное в результате множество обозначили символом 
и построили его булеан 
.
Тогда число элементов множества
равно …
построено множество , т.е. булеан множества (множество всех подмножеств множества ). Из этого булеана удалили пустое множество и все одноэлементные множества. Полученное в результате множество обозначили символом и построили его булеан .Тогда число элементов множества
равно … 
Дано множество 
и его подмножества 
, 
и 
, причём
, 
, 
.
Пусть
и 
– булеан множества 
, т.е. множество всех подмножеств множества 
.
Тогда истинно утверждение:
и его подмножества , и , причём , , .Пусть
и – булеан множества , т.е. множество всех подмножеств множества .Тогда истинно утверждение:
Даны числовые множества 
и 
.
Между элементами этих множеств
и 
введено бинарное отношение 
следующим образом: 
, если числа 
и 
взаимно просты. Тогда указанное бинарное отношение можно описать матрицей …
и . Между элементами этих множеств
и введено бинарное отношение следующим образом: , если числа и взаимно просты. Тогда указанное бинарное отношение можно описать матрицей … 
Между элементами числовых множеств 
и 
установлено бинарное отношение 
: 
, если 
, 
и число 
делит без остатка число 
.
Тогда графом этого бинарного отношения является …
и установлено бинарное отношение : , если , и число делит без остатка число .Тогда графом этого бинарного отношения является …
