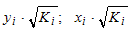Вопрос № 1026231 - Эконометрика
Проводится оценка параметров линейной модели парной регрессии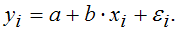 
Было выявлено, что остатки модели 
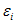являются гетероскедастичными и дисперсия остатков 
пропорциональна величине 
(
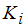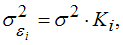где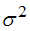 
– постоянная дисперсия). Оценку параметров предложено провести с помощью обобщенного метода наименьших квадратов, тогда преобразование исходных переменных модели 
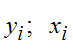будет иметь вид …
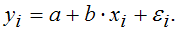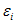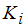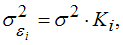Было выявлено, что остатки модели являются гетероскедастичными и дисперсия остатков пропорциональна величине ( где 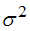– постоянная дисперсия). Оценку параметров предложено провести с помощью обобщенного метода наименьших квадратов, тогда преобразование исходных переменных модели 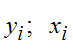будет иметь вид … 
Вопрос задал(а): Анонимный пользователь, 13 Ноябрь 2020 в 17:27
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 17:27
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 17:27
Похожие вопросы
Проводится оценка параметров линейной модели парной регрессии 
. Было выявлено, что остатки модели 
являются гетероскедастичными и дисперсия остатков 
пропорциональна величине 
(
, где 
– постоянная дисперсия). Оценку параметров предложено провести с помощью обобщенного метода наименьших квадратов, тогда преобразование исходных переменных модели 
будет иметь вид …
. Было выявлено, что остатки модели являются гетероскедастичными и дисперсия остатков пропорциональна величине (, где – постоянная дисперсия). Оценку параметров предложено провести с помощью обобщенного метода наименьших квадратов, тогда преобразование исходных переменных модели будет иметь вид … 
Проводится оценка параметров линейной модели парной регрессии 
. Было выявлено, что остатки модели 
являются гетероскедастичными и дисперсия остатков 
пропорциональна величине 
(
, где 
– постоянная дисперсия). Оценку параметров предложено провести с помощью обобщенного метода наименьших квадратов, тогда преобразование исходных переменных модели 
будет иметь вид …
. Было выявлено, что остатки модели являются гетероскедастичными и дисперсия остатков пропорциональна величине (, где – постоянная дисперсия). Оценку параметров предложено провести с помощью обобщенного метода наименьших квадратов, тогда преобразование исходных переменных модели будет иметь вид … 
Другие вопросы по предмету Эконометрика
Исходная регрессионная модель имеет вид 
Преобразование переменных вида 
используется в том случае, если предпосылки МНК ________ и оценка параметров проводится с помощью ________ метода наименьших квадратов.
Преобразование переменных вида используется в том случае, если предпосылки МНК ________ и оценка параметров проводится с помощью ________ метода наименьших квадратов.
нарушены; традиционного
не нарушены; традиционного
не нарушены; обобщенного
нарушены; обобщенного
Пусть y – издержки производства, 
– объем продукции, 
– основные производственные фонды, 
– численность работников. Известно, что в уравнении 
дисперсии остатков пропорциональны квадрату численности работников 
После применения обобщенного метода наименьших квадратов новая модель приняла вид
Тогда параметр 
в новом уравнении характеризует среднее изменение затрат …
– объем продукции, – основные производственные фонды, – численность работников. Известно, что в уравнении дисперсии остатков пропорциональны квадрату численности работников После применения обобщенного метода наименьших квадратов новая модель приняла вид
Тогда параметр в новом уравнении характеризует среднее изменение затрат …
на единицу продукции при увеличении трудоемкости продукции на единицу при неизменном уровне фондоемкости продукции
на работника при увеличении фондовооруженности труда на единицу при неизменном уровне производительности труда
на единицу продукции при увеличении фондоемкости продукции на единицу при неизменном уровне трудоемкости продукции
на работника при увеличении производительности труда на единицу при неизменном уровне фондовооруженности труда
Пусть y – издержки производства, 
– объем продукции, 
– основные производственные фонды, 
– численность работников. Известно, что в уравнении 
дисперсии остатков пропорциональны квадрату объема продукции 
.
Применим обобщенный метод наименьших квадратов, поделив обе части уравнения на
После применения обобщенного метода наименьших квадратов новая модель приняла вид 
. Тогда параметр 
в новом уравнении характеризует среднее изменение затрат на единицу продукции при увеличении …
– объем продукции, – основные производственные фонды, – численность работников. Известно, что в уравнении дисперсии остатков пропорциональны квадрату объема продукции .Применим обобщенный метод наименьших квадратов, поделив обе части уравнения на
После применения обобщенного метода наименьших квадратов новая модель приняла вид . Тогда параметр в новом уравнении характеризует среднее изменение затрат на единицу продукции при увеличении …
производительности труда при неизменном уровне фондовооруженности труда
фондовооруженности труда при неизменном уровне производительности труда
трудоемкости продукции при неизменном уровне фондоемкости продукции
фондоемкости продукции при неизменном уровне трудоемкости продукции
Установите соответствие между значением коэффициента линейной корреляции и характеристикой его значения:
1) 0,4 %place1%
2) -0,8 %place2%
3) 1 %place3%
1) 0,4 %place1%
2) -0,8 %place2%
3) 1 %place3%
на зависимый признак не влияют включенные в уравнение факторы
связь между признаками слабая
связь между признаками тесная
на зависимый признак влияют только включенные в уравнение факторы