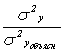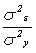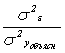Вопрос № 580322 - Эконометрика
Пусть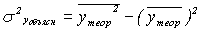 
- дисперсия зависимой переменной, объясненная уравнением регрессии; 
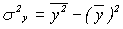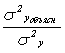
- общая дисперсия зависимой переменной;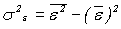 
- дисперсия факторов, неучтенных явно в модели. Тогда значение коэффициента детерминации можно рассчитать как
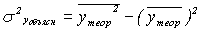- дисперсия зависимой переменной, объясненная уравнением регрессии; 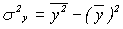- общая дисперсия зависимой переменной; 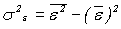- дисперсия факторов, неучтенных явно в модели. Тогда значение коэффициента детерминации можно рассчитать как 
Вопрос задал(а): Анонимный пользователь, 10 Ноябрь 2020 в 19:44
На вопрос ответил(а): Анастасия Степанова, 10 Ноябрь 2020 в 19:44
На вопрос ответил(а): Анастасия Степанова, 10 Ноябрь 2020 в 19:44
Похожие вопросы
Пусть 
- дисперсия зависимой переменной, объясненная уравнением регрессии; 
- общая дисперсия зависимой переменной; 
- дисперсия факторов, неучтенных явно в модели. Тогда значение коэффициента детерминации можно рассчитать по формуле …
- дисперсия зависимой переменной, объясненная уравнением регрессии; - общая дисперсия зависимой переменной; - дисперсия факторов, неучтенных явно в модели. Тогда значение коэффициента детерминации можно рассчитать по формуле … 
Пусть 
- дисперсия зависимой переменной, объясненная уравнением регрессии; 
- общая дисперсия зависимой переменной; 
- дисперсия случайных факторов. Тогда значение коэффициента детерминации можно рассчитать как
- дисперсия зависимой переменной, объясненная уравнением регрессии; - общая дисперсия зависимой переменной; - дисперсия случайных факторов. Тогда значение коэффициента детерминации можно рассчитать как 
Другие вопросы по предмету Эконометрика
Пусть 
, где y – фактическое значение зависимой переменной, 
- теоретическое , рассчитанное по уравнению значение зависимой переменной (объясненное уравнением регрессии), 
– ошибка модели. Тогда значение 
характеризует дисперсию …
, где y – фактическое значение зависимой переменной, - теоретическое , рассчитанное по уравнению значение зависимой переменной (объясненное уравнением регрессии), – ошибка модели. Тогда значение характеризует дисперсию …
случайных факторов
фактических значений независимой переменной
фактических значений зависимой переменной
зависимой переменной, объясненную уравнением регрессии
Пусть 
, где y – фактическое значение зависимой переменной, 
- теоретическое , рассчитанное по уравнению значение зависимой переменной (объясненное уравнением регрессии), 
– ошибка модели. Тогда значение 
характеризует дисперсию …
, где y – фактическое значение зависимой переменной, - теоретическое , рассчитанное по уравнению значение зависимой переменной (объясненное уравнением регрессии), – ошибка модели. Тогда значение характеризует дисперсию …
зависимой переменной, объясненную уравнением регрессии
случайных факторов
фактических значений независимой переменной
фактических значений зависимой переменной
Пусть 
, где y – фактическое значение зависимой переменной, 
- теоретическое , рассчитанное по уравнению значение зависимой переменной (объясненное уравнением регрессии), 
– ошибка модели (факторы, неучтенные явно в модели). Тогда значение 
характеризует дисперсию …
, где y – фактическое значение зависимой переменной, - теоретическое , рассчитанное по уравнению значение зависимой переменной (объясненное уравнением регрессии), – ошибка модели (факторы, неучтенные явно в модели). Тогда значение характеризует дисперсию …
фактических значений зависимой переменной
фактических значений независимой переменной
зависимой переменной, объясненную уравнением регрессии
неучтенных явно в модели факторов
Для парной линейной регрессионной модели коэффициент детерминации является мерой, позволяющей сравнить ...
средние значения фактора 
и результирующего признака 
и результирующего признака
последовательные значения автокорреляционной функции
вклад параметров регрессии 
и 
в вариацию результирующего признака 
и в вариацию результирующего признака
объяснение значений результирующего признака с помощью линии регрессии 
и с помощью прямой 
и с помощью прямой