Вопрос № 859959 - Математика
Пусть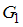 
– группа всех положительных рациональных чисел относительно операции обычного умножения; 
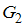– группа всех действительных чисел относительно операции обычного сложения.
Тогда отображение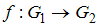
, определяемое соотношением 
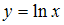, где 
, 
, …
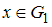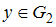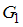– группа всех положительных рациональных чисел относительно операции обычного умножения; 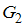– группа всех действительных чисел относительно операции обычного сложения.Тогда отображение
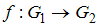, определяемое соотношением 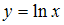, где , , …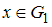
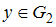Вопрос задал(а): Анонимный пользователь, 13 Ноябрь 2020 в 15:21
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 15:21
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 15:21
Похожие вопросы
Пусть 
– группа всех положительных рациональных чисел относительно операции обычного умножения; 
– группа всех действительных чисел относительно операции обычного сложения.
Тогда отображение
, определяемое соотношением 
, где 
, 
, …
– группа всех положительных рациональных чисел относительно операции обычного умножения; – группа всех действительных чисел относительно операции обычного сложения.Тогда отображение
, определяемое соотношением , где , , …
является эпиморфизмом
является автоморфизмом
не является гомоморфизмом
является мономорфизмом
Пусть 
– группа всех целых чисел относительно операции обычного сложения целых чисел.
Тогда подгруппой этой группы является …
– группа всех целых чисел относительно операции обычного сложения целых чисел.Тогда подгруппой этой группы является …
множество неотрицательных целых чисел
множество всех неположительных целых чисел
множество всех нечётных целых чисел
множество всех целых чисел, кратных числу 
Другие вопросы по предмету Математика
Множество 
, бинарная операция на котором определена таблицей
,
является группой с единичным элементом
(это группа симметрий правильного треугольника). Множество 
– подгруппа группы 
.
Тогда левым смежным классом группы
по подгруппе 
, порождённым элементом 
, является множество …
, бинарная операция на котором определена таблицей,является группой с единичным элементом
(это группа симметрий правильного треугольника). Множество – подгруппа группы .Тогда левым смежным классом группы
по подгруппе , порождённым элементом , является множество … 
Пусть 
и 
– группы, в которых бинарные операции обозначены символами 
и 
, операции взятия обратных элементов (унарные операции) обозначены 
и 
, а 
и 
– единичные элементы.
Пусть
– групповой морфизм (гомоморфизм группы 
в группу 
).
Тогда отображение
может не обладать свойством …
и – группы, в которых бинарные операции обозначены символами и , операции взятия обратных элементов (унарные операции) обозначены и , а и – единичные элементы.Пусть
– групповой морфизм (гомоморфизм группы в группу ).Тогда отображение
может не обладать свойством … 
(здесь 
– символ прообраза)
Пусть 
– знакопеременная группа.
Тогда элементом этой группы не является подстановка …
– знакопеременная группа.Тогда элементом этой группы не является подстановка …
Циклическая группа порядка 
имеет образующий элемент 
, при этом 
– единичный элемент циклической группы.
Тогда среди заданных множеств подгруппой циклической группы не является множество …
имеет образующий элемент , при этом – единичный элемент циклической группы.Тогда среди заданных множеств подгруппой циклической группы не является множество …
неверный ответ
