Дана система линейных уравнений с неизвестными. Пусть ранг матрицы этой системы равен а ранг расш...: ответ на тест 562059 - Математика
Дана система 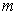 линейных уравнений с
линейных уравнений с 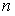 неизвестными. Пусть ранг матрицы этой системы равен
неизвестными. Пусть ранг матрицы этой системы равен 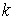 , а ранг расширенной матрицы системы равен
, а ранг расширенной матрицы системы равен 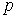 . Правильными утверждениями являются…
. Правильными утверждениями являются…
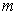 линейных уравнений с
линейных уравнений с 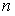 неизвестными. Пусть ранг матрицы этой системы равен
неизвестными. Пусть ранг матрицы этой системы равен 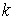 , а ранг расширенной матрицы системы равен
, а ранг расширенной матрицы системы равен 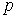 . Правильными утверждениями являются…
. Правильными утверждениями являются…
Вопрос задал(а): Анонимный пользователь, 10 Ноябрь 2020 в 18:32
На вопрос ответил(а): Анастасия Степанова, 10 Ноябрь 2020 в 18:32
На вопрос ответил(а): Анастасия Степанова, 10 Ноябрь 2020 в 18:32

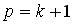 , то система не имеет решений
, то система не имеет решений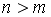 , то система имеет хотя бы одно решение
, то система имеет хотя бы одно решение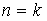 , то система совместна
, то система совместна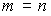 система может иметь бесконечное множество решений
система может иметь бесконечное множество решений