Вопрос № 1027057 - Математический анализ
Цена p (у.е.) на продукцию линейно падает с увеличением объема x (ед.) предъявления готовой продукции на рынке как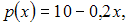 
а затраты С (у.е.) зависят от объема производства как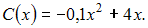 
Наибольшее значение прибыли равно ___ у.е.
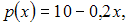а затраты С (у.е.) зависят от объема производства как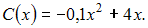 Наибольшее значение прибыли равно ___ у.е.
Вопрос задал(а): Анонимный пользователь, 13 Ноябрь 2020 в 17:28
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 17:28
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 17:28
Похожие вопросы
Цена p (у.е.) на продукцию линейно падает с увеличением объема x (ед.) предъявления готовой продукции на рынке как а затраты С (у.е.) зависят от объема производства как
Функция прибыли равна …
а затраты С (у.е.) зависят от объема производства как Функция прибыли равна …
Цена p (у.е.) на продукцию линейно падает с увеличением объема x (ед.) предъявления готовой продукции на рынке как 
а затраты С (у.е.) зависят от объема производства как 
Наибольшее значение прибыли равно ___ у.е.
а затраты С (у.е.) зависят от объема производства как Наибольшее значение прибыли равно ___ у.е.
Другие вопросы по предмету Математический анализ
Цена p (у.е.) на продукцию линейно падает с увеличением объема x (ед.) предъявления готовой продукции на рынке как 
а затраты С (у.е.) зависят от объема производства как 
Наибольшее значение прибыли равно _____ у.е.
а затраты С (у.е.) зависят от объема производства как Наибольшее значение прибыли равно _____ у.е.
Цена p (у.е.) на продукцию линейно падает с увеличением объема x (ед.) предъявления готовой продукции на рынке как 
а затраты С (у.е.) зависят от объема производства как 
Наибольшее значение прибыли равно _____ у.е.
а затраты С (у.е.) зависят от объема производства как Наибольшее значение прибыли равно _____ у.е.
Цена p (у.е.) на продукцию линейно падает с увеличением объема x (ед.) предъявления готовой продукции на рынке как а затраты С (у.е.) зависят от объема производства как
Пусть предприятие платит налог, который является акцизом со ставкой t, то есть
Установите соответствие между значениями ставки t и объемом производства, при котором достигается наибольшая прибыль.
1. t = 0,1
2. t = 0,3
3. t = 0,5
а затраты С (у.е.) зависят от объема производства как Пусть предприятие платит налог, который является акцизом со ставкой t, то есть
Установите соответствие между значениями ставки t и объемом производства, при котором достигается наибольшая прибыль.1. t = 0,1
2. t = 0,3
3. t = 0,5
29,0
28,0
29,5
28,5
27,5
Цена p (у.е.) на продукцию линейно падает с увеличением объема x (ед.) предъявления готовой продукции на рынке как а затраты С (у.е.) зависят от объема производства как
Пусть предприятие платит налог, который является акцизом со ставкой t, то есть
Установите соответствие между значениями ставки t и объемом производства, при котором достигается наибольшая прибыль.
1. t = 0,1
2. t = 0,3
3. t = 0,5
а затраты С (у.е.) зависят от объема производства как Пусть предприятие платит налог, который является акцизом со ставкой t, то есть
Установите соответствие между значениями ставки t и объемом производства, при котором достигается наибольшая прибыль.1. t = 0,1
2. t = 0,3
3. t = 0,5
19,0
18,0
19,5
18,5
17,5