Приведенное выражение представляет собой _________ для линейной двухфакторной модели регрессии.: ответ на тест 718582 - Эконометрика
Приведенное выражение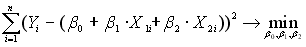
представляет собой _________ для линейной двухфакторной модели регрессии.
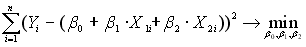представляет собой _________ для линейной двухфакторной модели регрессии.
Вопрос задал(а): Анонимный пользователь, 13 Ноябрь 2020 в 00:25
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 00:25
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 00:25
Похожие вопросы
Приведенное выражение
представляет собой _________ для линейной двухфакторной модели регрессии.
представляет собой _________ для линейной двухфакторной модели регрессии.
условие отсутствия автокорреляции остатков
систему нормальных уравнений
теорему Гаусса-Маркова
исходное положение метода наименьших квадратов
Для множественной линейной модели регрессии ... 
система нормальных уравнений метода наименьших квадратов представляет собой систему
система нормальных уравнений метода наименьших квадратов представляет собой систему 
линейных уравнений с 
неизвестными 
линейных уравнений с 
неизвестными 
линейных уравнений с 
неизвестными 
линейных уравнений с 
неизвестными Другие вопросы по предмету Эконометрика
Метод определения оценок параметров функции 
из условия минимизации выражения 
называется методом ...
из условия минимизации выражения называется методом ...
Исходное соотношение метода наименьших квадратов имеет вид ...
В качестве оценки вектора 
неизвестных коэффициентов регрессии принимают вектор 
, который _____ сумму квадратов отклонений наблюдаемых значений результативного признака от рассчитанных по модели.
неизвестных коэффициентов регрессии принимают вектор , который _____ сумму квадратов отклонений наблюдаемых значений результативного признака от рассчитанных по модели.
Запись вида
представляет собой систему нормальных уравнений для оценки параметров _______ модели регрессии.
представляет собой систему нормальных уравнений для оценки параметров _______ модели регрессии.
Все Предметы (168)
- Административное право
- Анализ финансово-хозяйственной деятельности
- Анатомия
- Английский язык
- Арбитражный процесс
- Архитектура
- Базы данных
- Безопасность жизнедеятельности
- Биология
- Ботаника
- Бухгалтерский учет
- Бухгалтерский финансовый учет
- Бюджетное право
- Возрастная анатомия
- Возрастная физиология
- Вычислительная математика
- Вычислительная техника
- Генетика
- География
- Геодезия
- Гидравлика
- Гистология, эмбриология и цитология
- Гражданское право
- Гражданское процессуальное право
- Демография
- Деньги, кредит, банки
- Детали машин и основы конструирования
- Диагностика готовности первокурсников к продолжению обучения
- Дискретная математика
- Естественнонаучная картина мира
- Защита растений
- Земельное право
- Земледелие
- Инженерная геодезия
- Инженерная геология
- Инженерная графика
- Инженерная и компьютерная графика
- Иностранный язык
- Информатика
- Информационные технологии в профессиональной деятельности
- Информационные технологии в юридической деятельности
- Информационные технологии управления
- История
- История государства и права
- История государства и права зарубежных стран
- История и философия науки
- История изучаемого региона
- История образования и педагогической мысли
- История политических и правовых учений
- История России
- История философии
- Коммерческое право
- Конституционное право зарубежных стран
- Конституционное право России
- Конструкция и проектирование летательных аппаратов
- Конфликтология
- Концепции современного естествознания
- Криминалистика
- Культурология
- Линейная алгебра
- Логика
- Макроэкономика
- Маркетинг
- Математика
- Математика и информатика
- Математический анализ
- Материаловедение
- Международное право
- Международное частное право
- Менеджмент
- Метрология, стандартизация и сертификация
- Механика грунтов
- Микробиология
- Микробиология и иммунология
- Микробиология, вирусология и иммунология
- Микроэкономика
- Мировая экономика
- Мировые информационные ресурсы
- Морфология животных
- Морфология сельскохозяйственных животных
- Налоговое право
- Наследственное право
- Национальная экономика
- Начертательная геометрия
- Начертательная геометрия, инженерная графика
- Немецкий язык
- Неорганическая химия
- Общая электротехника и электроника
- Обществознание
- Олимпиада математика, физика и информатика
- Основы безопасности жизнедеятельности
- Основы бухгалтерского учета
- Основы медицинских знаний и здорового образа жизни
- Основы почвоведения и сельскохозяйственного производства
- Основы права
- Основы социологии и политологии
- Основы специальной педагогики и психологии
- Основы теории цепей
- Основы философии
- Основы экономики
- Педагогика
- Политология
- Почвоведение
- Право социального обеспечения
- Правовая статистика
- Правоведение
- Правовое обеспечение профессиональной деятельности
- Правовое регулирование профессиональной деятельности
- Правоохранительные органы
- Прикладная механика
- Программирование
- Прокурорский надзор
- Пропедевтика внутренних болезней
- Психология
- Психология и педагогика
- Психология социально-правовой деятельности
- Радиотехнические цепи и сигналы
- Римское право
- Риторика
- Русский язык
- Русский язык и культура речи
- Сетевая экономика
- Сопротивление материалов
- Социальная психология
- Социология
- Статистика
- Стратегический менеджмент
- Теоретическая механика
- Теоретические основы электротехники
- Теория автоматического управления
- Теория вероятностей и математическая статистика
- Теория государства и права
- Теория дискретных устройств автоматики и телемеханики
- Теория и история физической культуры
- Теория механизмов и машин
- Теплотехника
- Теплоэнергетика
- Техническая механика
- Технология конструкционных материалов
- Технология социальной работы
- Токсикологическая химия
- Торговое законодательство зарубежных стран
- Трудовое право
- Уголовное право
- Физика
- Физиология и биохимия растений
- Физиология и этология животных
- Физиология растений
- Физическая культура
- Философия
- Финансовый менеджмент
- Финансы и кредит
- Французский язык
- Химия
- Экологические основы природопользования
- Экологическое право
- Экология
- Эконометрика
- Экономика
- Экономика организации (предприятия)
- Экономическая теория
- Экономический анализ
- Электрические машины и электропривод
- Электротехника и электроника
- Электроэнергетика
- Эпидемиология
- Этика деловых отношений
- Юридическая психология