Функция представлена таблицей Известно что на отрезке максимальное значение производной третьего ...: ответ на тест 860298 - Математика
Функция 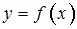 представлена таблицей
представлена таблицей
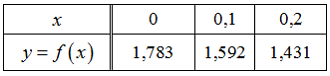
Известно, что на отрезке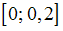 максимальное значение производной третьего порядка
максимальное значение производной третьего порядка 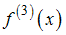 равно 12. В точке
равно 12. В точке 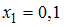 вычислено значение производной
вычислено значение производной 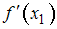 на основе интерполяционного полинома Лагранжа 2-й степени.
на основе интерполяционного полинома Лагранжа 2-й степени.
Тогда погрешность (округлённая до двух знаков после запятой) не превышает значения …
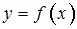 представлена таблицей
представлена таблицей
Известно, что на отрезке
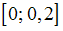 максимальное значение производной третьего порядка
максимальное значение производной третьего порядка 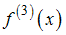 равно 12. В точке
равно 12. В точке 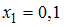 вычислено значение производной
вычислено значение производной 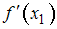 на основе интерполяционного полинома Лагранжа 2-й степени.
на основе интерполяционного полинома Лагранжа 2-й степени.Тогда погрешность (округлённая до двух знаков после запятой) не превышает значения …
Вопрос задал(а): Анонимный пользователь, 13 Ноябрь 2020 в 15:22
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 15:22
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 15:22
