Пусть на множестве определён предикат . Выражение истинно тогда и только тогда когда: ответ на тест 853005 - Математика
Пусть на множестве 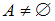 определён предикат
определён предикат 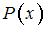 .
.
Выражение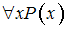 истинно тогда и только тогда, когда …
истинно тогда и только тогда, когда …
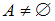 определён предикат
определён предикат 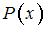 .
. Выражение
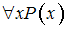 истинно тогда и только тогда, когда …
истинно тогда и только тогда, когда …
Вопрос задал(а): Анонимный пользователь, 13 Ноябрь 2020 в 15:19
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 15:19
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 15:19

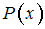 имеет хотя бы одно ложное значение на множестве
имеет хотя бы одно ложное значение на множестве 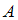
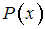 является тождественно истинным предикатом
является тождественно истинным предикатом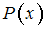 имеет хотя бы одно истинное значение на множестве
имеет хотя бы одно истинное значение на множестве 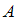
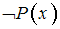 является тождественно истинным предикатом
является тождественно истинным предикатом