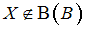Расставьте предложенные соотношения в правильной последовательности и получите обоснование неравенст...: ответ на тест 853009 - Математика
Расставьте предложенные соотношения в правильной последовательности и получите обоснование неравенства
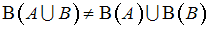 ,
,
где, например,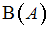 – булеан множества
– булеан множества 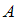 , т.е. множество всех подмножеств множества
, т.е. множество всех подмножеств множества 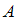 (здесь
(здесь 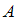 и
и 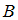 – произвольные подмножества универсального множества
– произвольные подмножества универсального множества 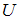 ).
).
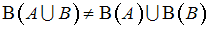 ,
,где, например,
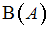 – булеан множества
– булеан множества 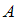 , т.е. множество всех подмножеств множества
, т.е. множество всех подмножеств множества 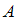 (здесь
(здесь 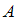 и
и 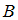 – произвольные подмножества универсального множества
– произвольные подмножества универсального множества 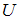 ).
).
Вопрос задал(а): Анонимный пользователь, 13 Ноябрь 2020 в 15:19
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 15:19
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 15:19

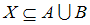 и
и 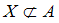 и
и 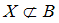
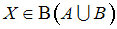 , т.е.
, т.е. 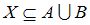
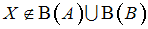
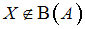 и
и