Имеется модель регрессии характеризующая зависимость y от x Известны среднеквадратичные отклонения ...: ответ на тест 907077 - Эконометрика
Имеется модель регрессии, характеризующая зависимость y от x  Известны среднеквадратичные отклонения для переменных и количество наблюдений:
Известны среднеквадратичные отклонения для переменных и количество наблюдений: 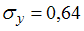 ,
,  и
и  Вычислите коэффициент корреляции
Вычислите коэффициент корреляции  и сделайте вывод относительно тесноты связи между y и x.
и сделайте вывод относительно тесноты связи между y и x.
 Известны среднеквадратичные отклонения для переменных и количество наблюдений:
Известны среднеквадратичные отклонения для переменных и количество наблюдений: 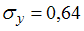 ,
,  и
и  Вычислите коэффициент корреляции
Вычислите коэффициент корреляции  и сделайте вывод относительно тесноты связи между y и x.
и сделайте вывод относительно тесноты связи между y и x.
Вопрос задал(а): Анонимный пользователь, 13 Ноябрь 2020 в 16:09
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 16:09
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 16:09

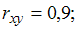 теснота связи сильная, зависимость прямая
теснота связи сильная, зависимость прямая теснота связи средняя, зависимость обратная
теснота связи средняя, зависимость обратная теснота связи средняя, зависимость прямая
теснота связи средняя, зависимость прямая теснота связи сильная, зависимость обратная
теснота связи сильная, зависимость обратная