Пусть – произвольное множество универсальное – произвольное подмножество – дополнения множества ...: ответ на тест 859820 - Математика
Пусть 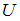 – произвольное множество (универсальное),
– произвольное множество (универсальное), 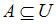 – произвольное подмножество,
– произвольное подмножество, 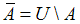 – дополнения множества
– дополнения множества 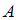 до множества
до множества 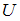 (разность множеств
(разность множеств 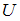 и
и 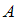 ).
).
Если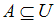 ,
, 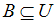 и
и 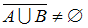 , то доказательство включения
, то доказательство включения 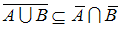 образует последовательность приведённых эквивалентностей …
образует последовательность приведённых эквивалентностей …
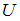 – произвольное множество (универсальное),
– произвольное множество (универсальное), 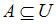 – произвольное подмножество,
– произвольное подмножество, 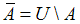 – дополнения множества
– дополнения множества 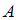 до множества
до множества 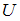 (разность множеств
(разность множеств 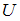 и
и 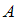 ).
).Если
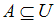 ,
, 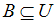 и
и 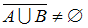 , то доказательство включения
, то доказательство включения 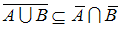 образует последовательность приведённых эквивалентностей …
образует последовательность приведённых эквивалентностей …
Варианты ответов
-
По определению операции пересечения, соотношение
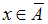 и
и 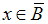 эквивалентно (равносильно) соотношению
эквивалентно (равносильно) соотношению 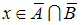
(кратко: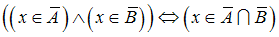 ).
).
-
Учитывая определение дополнения, можно утверждать, что соотношение
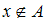 и
и 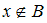 равносильно (эквивалентно) соотношению
равносильно (эквивалентно) соотношению 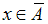 и
и 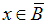
(кратко: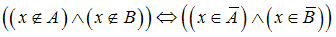 ).
).
-
Из определения операции дополнения множества следует, что утверждения
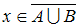 и
и 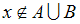 эквивалентны (равносильны)
эквивалентны (равносильны)
(кратко: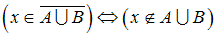 ).
).
-
Утверждение
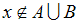 эквивалентно (равносильно) утверждению
эквивалентно (равносильно) утверждению 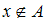 и
и 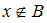 , что непосредственно следует из определения операции объединения множеств
, что непосредственно следует из определения операции объединения множеств
(кратко: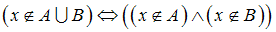 ).
).
Правильный ответ
Вопрос задал(а): Анонимный пользователь, 13 Ноябрь 2020 в 15:21
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 15:21
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 15:21
