Вопрос № 886977 - Математика
Пусть О – центр правильного 2011- угольника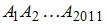 
, а Х – произвольная точка. Во сколько раз длина суммы векторов, соединяющих точку Х с вершинами многоугольника, больше длины вектора, соединяющего точку Х с точкой О?
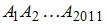, а Х – произвольная точка. Во сколько раз длина суммы векторов, соединяющих точку Х с вершинами многоугольника, больше длины вектора, соединяющего точку Х с точкой О?
Вопрос задал(а): Анонимный пользователь, 13 Ноябрь 2020 в 15:36
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 15:36
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 15:36
Похожие вопросы
Пусть О – центр правильного 2011- угольника 
, а Х – произвольная точка. Во сколько раз длина суммы векторов, соединяющих точку Х с вершинами многоугольника, больше длины вектора, соединяющего точку Х с точкой О?
, а Х – произвольная точка. Во сколько раз длина суммы векторов, соединяющих точку Х с вершинами многоугольника, больше длины вектора, соединяющего точку Х с точкой О?
Пусть О – центр правильного 2011- угольника 
, а Х – произвольная точка. Во сколько раз длина суммы векторов, соединяющих точку Х с вершинами многоугольника, больше длины вектора, соединяющего точку Х с точкой О?
, а Х – произвольная точка. Во сколько раз длина суммы векторов, соединяющих точку Х с вершинами многоугольника, больше длины вектора, соединяющего точку Х с точкой О? Другие вопросы по предмету Математика
Даны три вершины треугольника 
, 
и 
Найти сумму координат точки пересечения плоскости 
с прямой, проходящей через начало координат и центр окружности, описанной около треугольника 
, и Найти сумму координат точки пересечения плоскости с прямой, проходящей через начало координат и центр окружности, описанной около треугольника
В треугольнике 
. На стороне 
отмечена точка M так, что 
. Обозначим: 
.
Найти
, если 
и 
.
. На стороне отмечена точка M так, что . Обозначим: . Найти
, если и .
Пусть 
Рассмотрим произвольное разбиение отрезка [−3; 3] на n элементарных участков: 
Для каждого такого разбиения составим сумму
Наибольшее значение S равно …
Рассмотрим произвольное разбиение отрезка [−3; 3] на n элементарных участков: Для каждого такого разбиения составим сумму
Наибольшее значение S равно …
Функция 
удовлетворяет условиям:
; 
Тогда
равно …
удовлетворяет условиям: ; Тогда
равно …