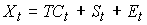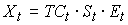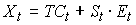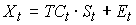Пусть – значения временного ряда – тренд-циклическая компонента этого ряда – сезонная компонента – ...: ответ на тест 719760 - Эконометрика
Пусть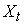 
– значения временного ряда, 
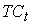– тренд-циклическая компонента этого ряда, 
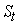– сезонная компонента, 
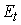– случайная компонента. Тогда общий вид аддитивной модели временного ряда можно представить как …
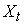– значения временного ряда, 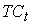– тренд-циклическая компонента этого ряда, 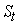– сезонная компонента, 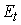– случайная компонента. Тогда общий вид аддитивной модели временного ряда можно представить как … 
Вопрос задал(а): Анонимный пользователь, 13 Ноябрь 2020 в 00:25
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 00:25
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 00:25