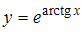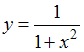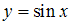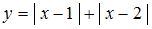Вопрос № 860015 - Математика
Пусть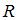 
– множество действительных чисел с естественной топологией (открытыми множествами являются всевозможные интервалы 
, 
, 
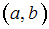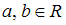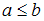, и любые объединения таких интервалов).
Рассматриваются отображения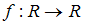
.
Тогда открытым является отображение …
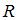– множество действительных чисел с естественной топологией (открытыми множествами являются всевозможные интервалы 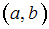, , 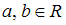, 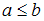и любые объединения таких интервалов).Рассматриваются отображения
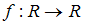.Тогда открытым является отображение …
Вопрос задал(а): Анонимный пользователь, 13 Ноябрь 2020 в 15:21
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 15:21
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 15:21
Похожие вопросы
Пусть 
– множество действительных чисел с естественной топологией (открытыми множествами являются всевозможные интервалы 
, 
, 
, и любые объединения таких интервалов).
Рассматриваются отображения
.
Тогда открытым является отображение …
– множество действительных чисел с естественной топологией (открытыми множествами являются всевозможные интервалы , , , и любые объединения таких интервалов).Рассматриваются отображения
.Тогда открытым является отображение …
Пусть на множестве 
действительных чисел определены:
1)
– естественная топология (открыты любые интервалы и любые объединения интервалов);
2)
– дискретная топология (открыты все подмножества);
3)
– тривиальная топология (открыты только множества 
и 
),
т.е. заданы топологические пространства
, 
и 
на одном и том же множестве-носителе.
Тогда гомеоморфизмом является отображение …
действительных чисел определены:1)
– естественная топология (открыты любые интервалы и любые объединения интервалов);2)
– дискретная топология (открыты все подмножества);3)
– тривиальная топология (открыты только множества и ),т.е. заданы топологические пространства
, и на одном и том же множестве-носителе.Тогда гомеоморфизмом является отображение …
, 
, 
, 
, 
Другие вопросы по предмету Математика
Пусть на множестве действительных чисел определены:
1) – естественная топология (открыты любые интервалы и любые объединения интервалов);
2) – дискретная топология (открыты все подмножества);
3) – тривиальная топология (открыты только множества и ),
т.е. заданы топологические пространства, и на одном и том же множестве-носителе.
Тогда гомеоморфизмом является отображение …
действительных чисел определены:1)
– естественная топология (открыты любые интервалы и любые объединения интервалов);2)
– дискретная топология (открыты все подмножества);3)
– тривиальная топология (открыты только множества и ),т.е. заданы топологические пространства
, и на одном и том же множестве-носителе.Тогда гомеоморфизмом является отображение …
, , , ,
Компактными топологическими пространствами являются …
, где 
– естественная топология множества 
действительных чисел (открыты все интервалы и любые их объединения) 
, где 
, где 
– дискретная топология на множестве 
. 
, где 
, 
– топология, индуцированная на 
естественной топологией на 
Пусть 
– компактное пространство, 
– хаусдорфово пространство, 
– непрерывное отображение.
Тогда это отображение является …
– компактное пространство, – хаусдорфово пространство, – непрерывное отображение.Тогда это отображение является …
открыто-замкнутым отображением
открытым отображением
гомеоморфизмом
замкнутым отображением
На плоскости 
задана метрика
.
Тогда компактом в метрическом пространстве
является множество …
задана метрика.Тогда компактом в метрическом пространстве
является множество … 
, где
